How important are statistics for science? Very
Mark Twain popularized the term “lies, damned lies and statistics” and this phrase has certainly stuck in our collective psychology. Statistics can certainly be used to argue things in different ways but in science they hold a much more important role.
One primary example of the importance of statistics is in the development of drugs. Clinical trials require the use of statisticians to help and determine the risks associated with a drug. This of course is incredibly important in the risk analysis that takes place for the drug. The FDA has to determine if the benefits of this new drug outweigh the risks before allowing it to go to market and often they have to make the determination based on a few trials, with a pretty small number of people in each trial. So using statistics we can usually do a pretty good job of pulling out how risky it will be in the general population, from a small sample size (assuming the sample size isn’t biased, which for the most part they go to great lengths to ensure is the case).
Statistics come up in more and surprising ways in science. For instance, when they are discussing results from the Large Hadron Collider (LHC) in Europe, they only present the results if they are within the 5 sigma level. This means that they are confident of their results to within 5 standard deviations of the mean value. What this means is that they are very confident that their results were not produced by random coincidence, you would only expect this coincidence to happen once in about 3.5 million tries. Of course this is determined by statistics.
Statistics are important in science because many things that occur in nature are stochastic, meaning that even if you knew the starting values (something that would itself be impossible to determine at least with current technology) you would not know with certainty what would happen next, you could only get the probabilities of different things happening next. This is something that disturbed Einstein about Quantum Mechanics for instance, because he felt that Quantum systems should be non-stochastic (or deterministic).
Stochastic systems then require statistics as a vital tool for their study. Surprisingly, if you understand the statistics behind a stochastic system you can gain considerable insight into the system. You may not be able to predict exactly what the system will do next, but you certainly can predict what the system will do on average, or how likely the system is to deviate from its average values.
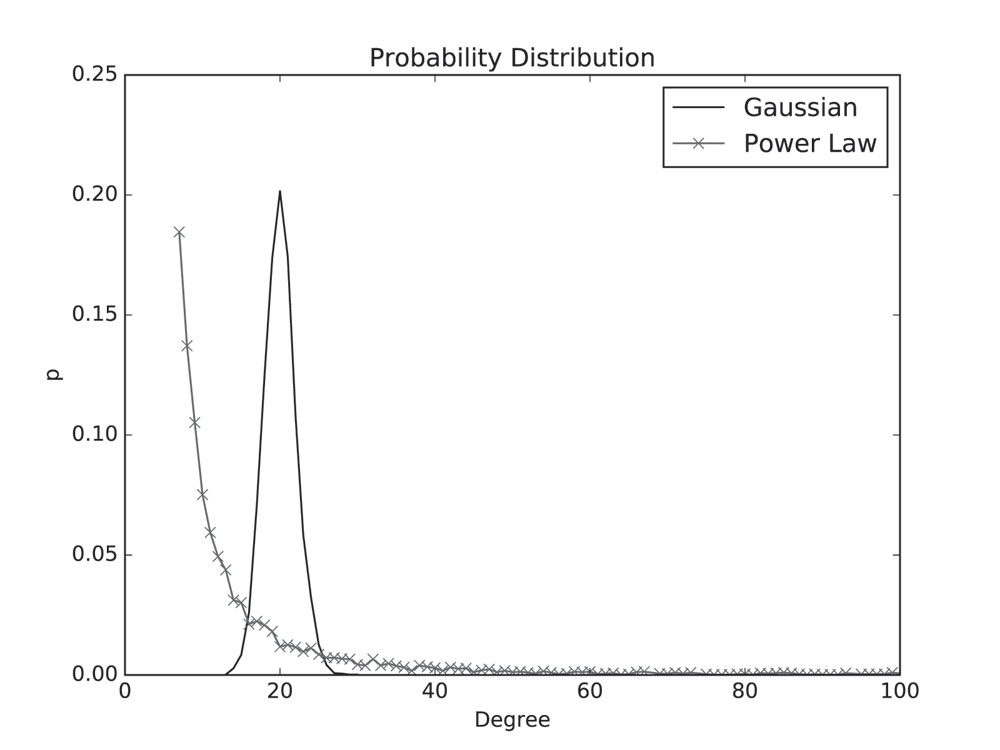
Of course knowledge of the underlying probabilities is important, if the distribution is unknown it is often assumed to be Gaussian, as many systems are approximately Gaussian, but this assumption can be bad if the probability distribution is significantly different from Gaussian, such as a power law distribution (you can see the power law distribution in the figure vs a Gaussian distribution). We have a mathematical tool now which allows us to avoid assumptions about the underlying probability distribution: information theory. But information theory still relies heavily on statistics.
So a reasonably good understanding of statistics has become necessary, at least to do mathematical work in the sciences. And this makes statistics very important.





